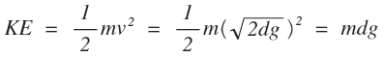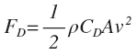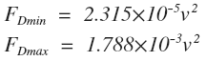It’s been a long time since I’ve posted anything on here. Life got in the way (as it tends to). One thing I would like to do more of here is explaining things. I am a teacher, after all. So starting today, whenever I get a chance I’m going to answer some common questions or address some misconceptions that are out there. I apologize that this one ended up being a little bit maths-intensive. I’ll try to limit that in the future as much as possible.
Question: Can a penny dropped off the roof of a tall building kill someone standing on the street below?
Answer: No. Not even if we were to remove the atmosphere. Without the atmosphere, a falling penny would be in a state of free fall in which the only force acting on it is gravity pulling it down toward the ground. A modern penny, with its zinc center and copper core, has a mass of 2.5000 g according to the US mint. Let’s say this penny is dropped from the Empire State Building, specifically from the 102nd floor observatory 1,224 feet (373.0752 meters). A penny dropped from this height in the absence of atmosphere would hit the ground with a speed of just over 120 meters per second (around 265mph).
Notice that nowhere in this calculation does the mass or weight of the penny appear. That is because the final speed of an object in free fall is independent of how much that object weighs. In perfect free fall, every object dropped from the 102nd floor of the Empire State Building would reach this speed before it hit the ground, regardless of its weight or shape.
But this does not mean that the mass of the penny is irrelevant, even in this atmosphere-less approximation. The mass of the penny may not matter when finding its final speed, but it certainly matters to the person standing underneath it, because the mass of the penny determines how much energy the penny has when it hits the ground. A penny moving at that speed would have around 18 Joules of energy, which is about as much energy as a 60-Watt light bulb uses in twenty seconds.
Finding an exact number for the amount of energy or pressure required to fracture or break a human skull is difficult (not many people willing to test it out, after all), but the lowest estimate I’ve found is 45 Joules, so even neglecting air resistance the penny just doesn’t have enough mass to kill someone when dropped off the roof of a building.
So let’s go higher. What if we dropped the penny out of an airplane flying at a typical cruising altitude of 30,000 feet (9,144 meters)? I could repeat the calculations, but there is no need to considering the kinetic energy of a falling object increases linearly with its drop height (see the equation below for proof and note you could prove the same thing using conservation of energy).
Going from 1,224 feet to 30,000 feet is an increase of 24.5 times, meaning the penny would have that much more energy when dropped from the plane than it would when dropped from the building. This would give us an energy of 442.9 Joules, well above our minimum requirement to bust some poor soul’s skull open like a melon.
So does this mean that a penny dropped from a sufficient height can actually kill someone? Alas, no. Keep in mind, we ignored the atmosphere when performing our calculations, and if we were to perform this test in a place without air, suffocation would kill the person long before we could even drop the penny. In order to give an actual answer, we must take into account the effects of air resistance.
You may wonder why exactly it matters whether there is atmosphere or not, and that’s because, for the most part in your life, it doesn’t. We’re so accustomed to being surrounded by atmosphere that most of us tend to think of it as empty space. You can’t see it, and if you reach out your hand you don’t feel it, but that doesn’t mean nothing’s there.
You can feel this for yourself if you swing your hand fast enough—you’ll be able to feel the air being pushed out of the way. A better (although slightly more dangerous example of this) is to stick your hand out of the window of a moving vehicle. If the vehicle is moving fast enough, you can feel the air pushing your hand back. That is the force of air resistance that slows down a falling penny.
Air is a fluid, a term often incorrectly used interchangeably with liquid in daily life (as a side note, it is this misuse of the term that leads to some people believing that glass is a liquid, when it is actually a solid fluid). In physics, a fluid is just anything that flows, and that’s exactly what air does. The space that looks empty to us is filled with air molecules—nitrogen and oxygen and carbon dioxide among many others. In order for an object to move through the air, it must first push these molecules out of its way. Because of Newton’s 3rd Law, the air molecules push back on the moving object with equal force, causing it to slow down.
If you’ve ever tried to wade through water then you’ve felt this force before, known as a drag force. Water is a much denser fluid than air and thus pushes on you much more when you try to displace it. And the faster you try to move, the more force you feel pushing you back because you’re trying to displace more of the fluid at a time.
Applying this back to our murderous penny, the air pushes up on the penny with a resistive force that gets stronger the faster the penny moves. The equation for air resistance, shown below, gives the relationship between the force of drag an object experiences and its speed.
Plugging in values for the drag coefficient of a flat disk, the density of air, and the dimensions of a penny as given by the US mint, we can calculate that the force of air resistance acting on the penny should be somewhere between the two values shown below (the minimum value assumes the penny fell the whole way with its thin side pointing down while the maximum value assumes it was flat-side down the whole time). Both of these cases are extremely unlikely, but we’ll use the numbers, just to prove our point.
We now have two forces acting on our penny—gravity pulling it down toward the ground, and air resistance pushing it back up. The gravitational force is constant (the weight of the penny, 0.0245 newtons) while the drag force increases as the penny gains speed. Eventually these two forces will equal each other, and the penny will enter a state of dynamic equilibrium (equilibrium because all of the forces acting on it balance each other out, dynamic because the penny happened to be moving when the forces became equal and thus will continue to move).
Once the penny enters equilibrium, the air will be pushing it up just as hard as gravity is pulling it down. As a result, the penny’s speed will become constant. We have a special name for the speed at which this happens: terminal velocity. Once a falling object reaches its terminal velocity, it stops accelerating and just falls with that speed until it hits the ground. And unlike objects in free fall which we discussed before, the terminal velocity of an object does depend on its weight. A heavier object will fall faster than a lighter one because it has a higher terminal velocity.
Using the two values for the drag force above, we can calculate the range of our penny’s terminal velocity to be between 10 and 85 meters-per-second (21.6 and 190 miles per hour). Notice that the minimum value of the drag force leads to the maximum terminal velocity.
Given these results, it makes no difference whether the penny is dropped from the top of the Empire State building, from a plane, or even from outer space because in all of these cases the penny will reach its terminal velocity before it hits the ground.
If you would like to look at drag forces for yourself, I’d recommend a simple experiment. All you need are a few clear glasses or bottles and some liquids of different densities (regular water, salt water, mineral oil, vinegar, even clear alcohols can work well for this, and taller glasses will give you a better chance to see what is happening). Drop the same object into each fluid and see which ones slow it down the most. Drop objects of different weights into the fluids and see which ones fall fastest. Change the shape of your weights by using something like aluminum foil and see how the geometry of the object affects how quickly it falls. If you have a tall enough glass or a light enough object, see if you can spot the moment it hits terminal velocity.